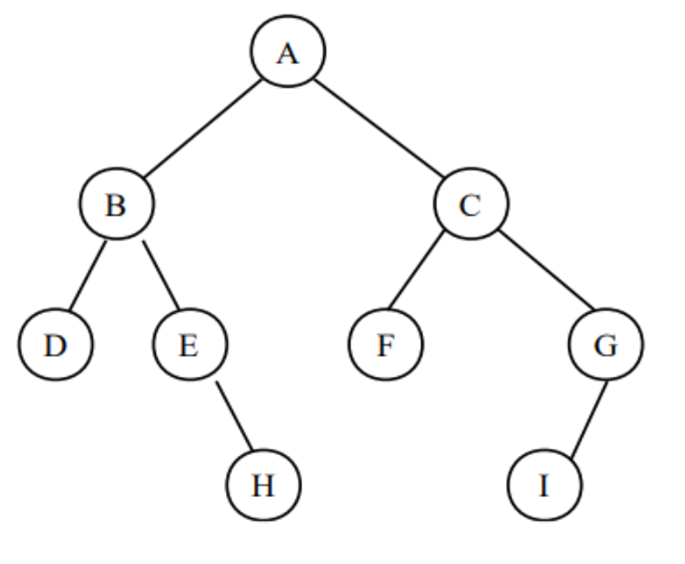
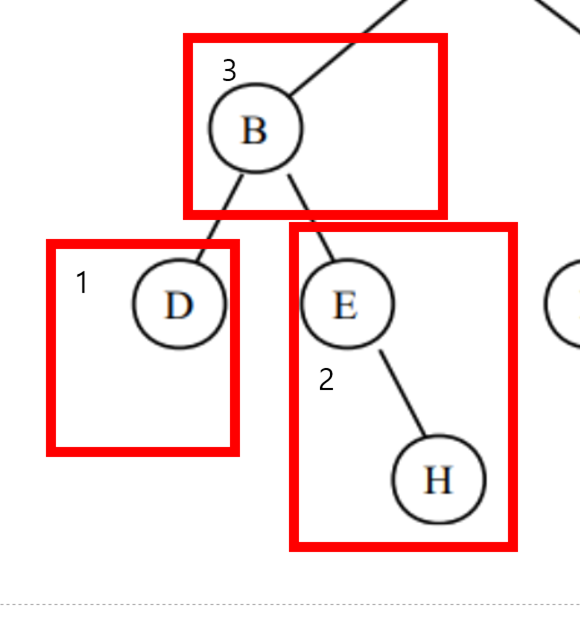
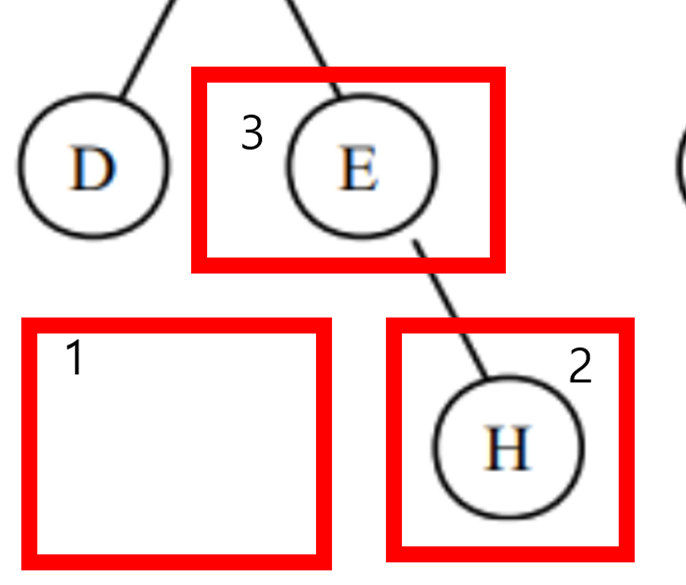
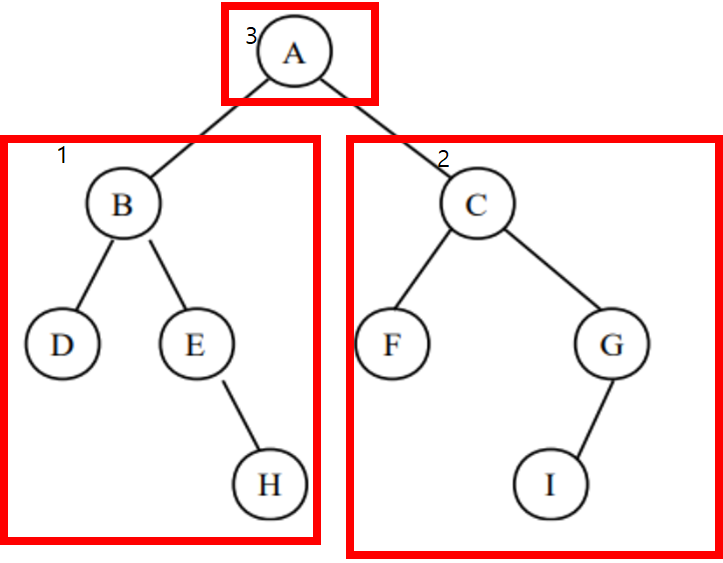
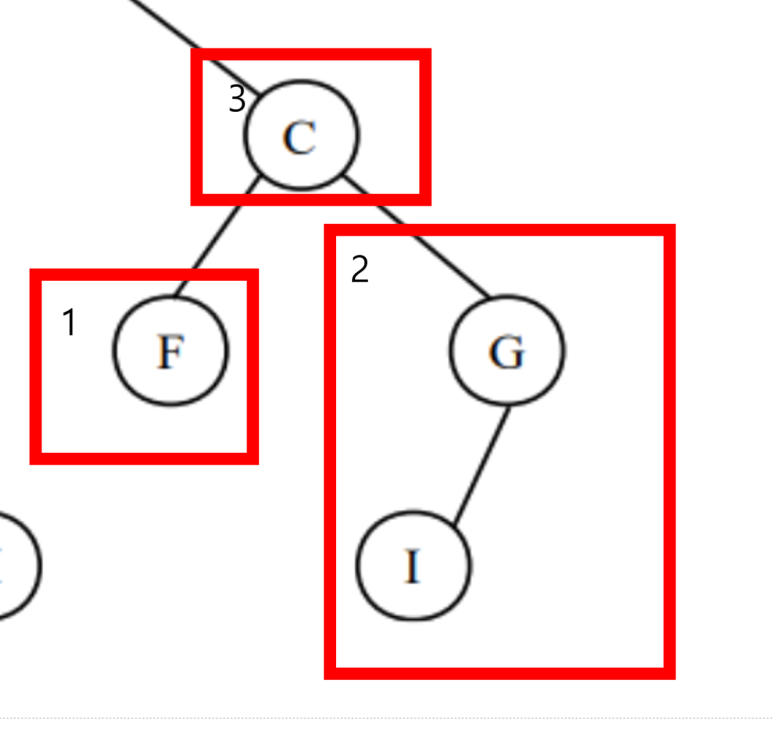
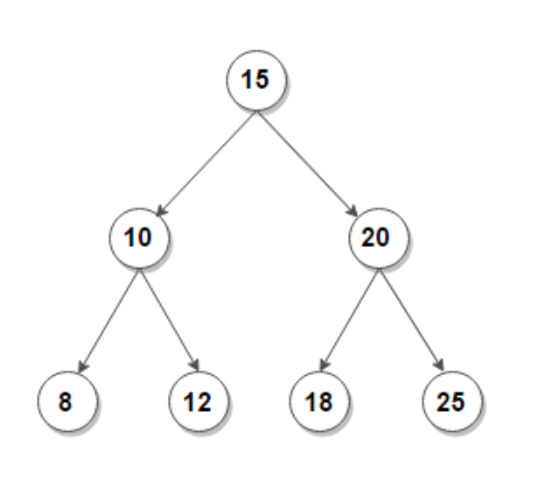
15가 루트 // 10(왼쪽 서브트리 ) < 15(루트)<20(오른쪽 서브트리)
하위 트리도 정의를 적용해보면 맞는걸 확인 가능하다
장점은 계산 복잡성이 O(logn)으로 빠르다
배열은 순차적으로 모든 데이터를 확인하며 나아가는 데에 반해서,
이진 탐색 트리는 서치 과정에서 탐색 해야하는 데이터를 줄여 나가기 때문에
데이터 검색 속도에서 더 높은 기댓값을 가진다.
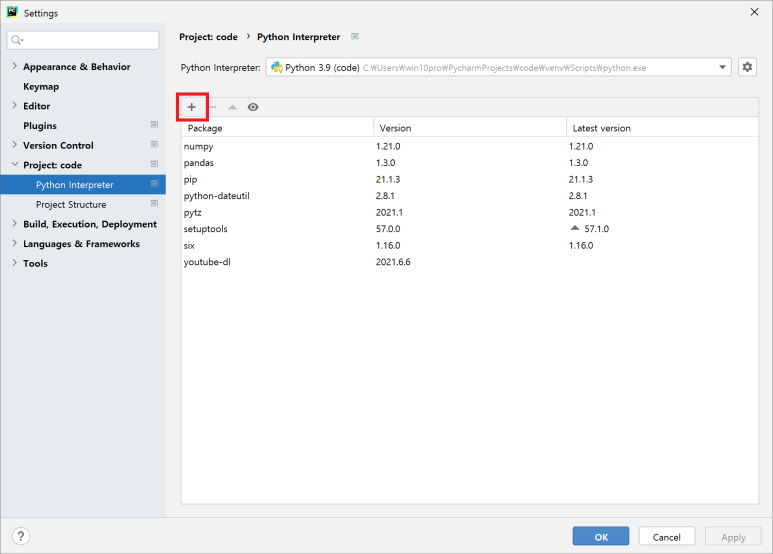
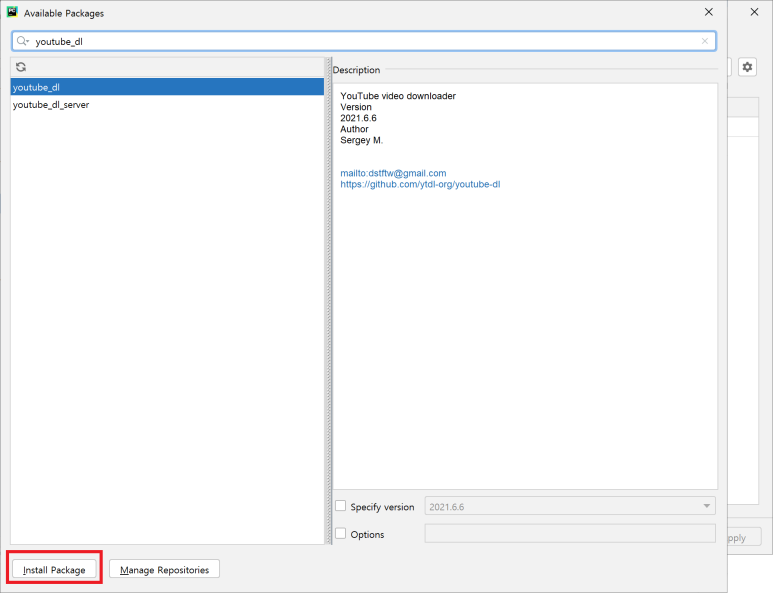
구현(파이썬이라 들여쓰기가 안맞을수 있어요)
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class Tree: # Binary Search Tree
def __init__(self):
self.head = None
def insert(self, value):
if self.head is None:
self.head = Node(value)
else:
node = self.head
while True:
if value < node.value:
if node.left is None:
node.left = Node(value)
break
else:
node = node.left
else:
if node.right is None:
node.right = Node(value)
break
else:
node = node.right
def delete(self, value):
if self.head is None:
return False
node = self.head
parent = self.head
check = False
while node:
if value == node.value:
check = True
break
elif value < node.value:
parent = node
node = node.left
else:
parent = node
node = node.right
if not check:
return False
# Case1 No Child
if node.left is None and node.right is None:
if value < parent.value:
parent.left = None
else:
parent.right = None
# Case2 Have a One Child
elif node.left and node.right is None:
if value < parent.value:
parent.left = node.left
else:
parent.right = node.left
elif node.left is None and node.right:
if value < parent.value:
parent.left = node.right
else:
parent.right = node.right
# Case3 Have Two Child
elif node.left and node.right:
current, child = node, node.right
while child.left:
current, child = child, child.left
node.value = child.value
if current != node:
if child.right:
current.left = child.right
else:
current.left = None
else:
node.right = child.right
def search(self, value):
if self.head is None:
return False, None
depth = 0
node = self.head
while True:
if value == node.value:
return True, depth
else:
if value < node.value:
node = node.left
else:
node = node.right
if node is None:
return False, None
depth += 1
def show(self, node, depth=0):
if node is None:
return
print(node.value, depth)
self.show(node.left, depth+1)
self.show(node.right, depth+1)
def print(self):
self.show(self.head)
tree = Tree()
tree.insert(5)
tree.insert(7)
tree.insert(1)
tree.insert(2)
tree.insert(8)
tree.insert(3)
tree.insert(4)
tree.insert(6)
tree.insert(9)
tree.print()
result = tree.search(5)
print(result)
print()
tree.delete(7)
tree.print()